La Logica Booleana
Le LB e nella gestione delle Reti Logiche
Quello che vogliamo mostrarvi in questo ultimo nostro passo è come la LB viene utilizzata dal punto di vista pratico e non solo teorico. Prima di tutto, però, è importante stabilire a cosa serve la Logica Booleana. Una vita non basterebbe a dire in quali infiniti ambiti venga utilizzata la LB, e ciò che vi mostriamo è solo un milionesimo di questi.
Possiamo dire con certezza che la LB viene utilizzata almeno in 3 ambiti:
1. Minimizzazione degli Stati di un Automa
Gli Automi a Stati sono modelli che meglio rappresentano un Sistema Automatico o Automa a Stati. Per chiarire il concetto pensate ad un ascensore, quello è un Automa a Stati dove gli stati sono i piani del palazzo. Attraverso la LB è possibile progettare Automi che abbiano costi poco elevati in termini di numero di Stati.
Le Macchine Sequenziali (Flip-Flop, Memorie, Contatori) sono per esempio sistemi di elaborazione che realizzano operazioni differenti a seconda dello "stato precedente" del Sistema. Una volta premuto il tasto nell'ascensore, esso dovrà calcolare quanti piani ("Stati") percorrere per arrivare e portarvi a destinazione.
2. Analisi e Sintesi delle Macchine Combinatorie
La LB si intravede anche nella realizzazione e progettazione di Macchine Combinatorie.
Le Macchine Combinatorie (Multiplexer, Demultiplexer, Decodificatori, Sommatori) sono sistemi di elaborazione hardware che realizzano operazioni anche complesse a seconda del valore che assumono gli ingressi e non godono del concetto di Stato in quanto eseguono operazione in cui non è necessario conoscere lo stato precedente. La LB aiuta la comprensione e la sintesi per poter rilevare guasti o progettare elementi sostitutivi.
3. Gestione delle Reti Logiche
Le Reti Logiche sono circuiti "logici" rappresentativi di circuiti elettronici fisici reali e la LB viene impiegata per gestire, rendere più efficienti, semplificare e progettare in modo più semplice tali circuiti. Una Rete Logica è costituita da un numero generalmente elevato di cosiddette Porte Logiche (Funzioni Booleane semplici), ognuna delle quali può rappresentare una sola delle Operazioni Booleane (AND, OR, NOT) che abbiamo appena visto, e di ingressi (variabili booleane). Ogni Porta Logica (AND, OR, NOT) ha inoltre la sua funzione e un suo simbolo grafico come si vede dalla figura sottostante.
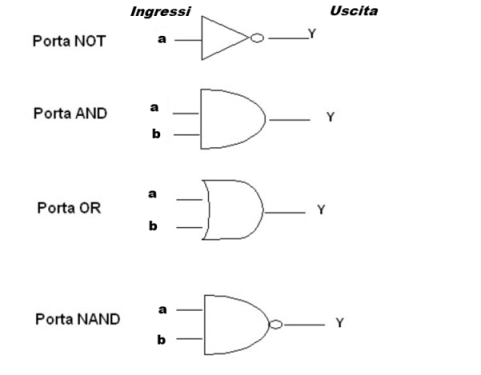
L'uscita Y di una Rete Logica complessa è nella maggior parte dei casi un insieme valori booleani del tipo "0000...0" oppure per esempio del tipo "10010..1", con tanti bit a seconda del numero di ingressi. In altri termini, una Rete Logica realizza tipicamente una Funzione Booleana
Y = f (A,B,C,..,Z)
dove (A,B,C,..,Z) sono gli ingressi ovvero le variabili booleane e Y l'uscita. Nel seguente esempio vi mostriamo l'esempio grafico di una Rete Logica e la sua Funzione Booleana "associata".
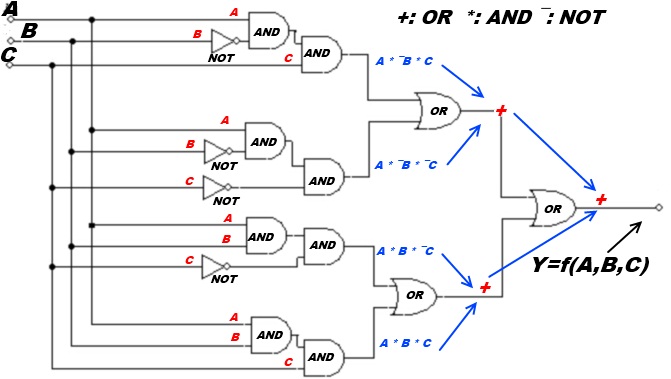
Provate ad inserire i vostri valori agli ingressi e verificate la vostra uscita Y!
Una Rete Logica può essere più o meno complessa a seconda del numero di ingressi (variabili booleane) e del numero di Porte che contiene. Essa è infatti tanto più complessa, quanti più sono gli ingressi e le porte utilizzate per realizzarla.
Il nostro lavoro si conclude qui, ora potete provare a progettare una Rete Logica anche voi ed eventualmente approfondire le vostre conoscenze!!! In bocca al lupo!

